Linear Regression

Linear Methods for Regression

선형회귀는 통계적 학습의 고전적인 방법이다. 하지만 문학에서의 고전 명작과 마찬가지로 현대의 수많은 머신러닝 기법들의 가장 기초가 된다. 또한 Simple is best 라는 말과 같이, 때로는 선형관계가 명확한 데이터에서 가장 효율적으로 작동하기도 한다. 이번 포스팅에서는 선형회귀의 기본이 되는 최소제곱법과 각종 규제법을 살펴보고자 한다.

최소제곱법^{Least Squares}

$p$개의 특성을 갖는 $n$개의 데이터가 각각 벡터(Input Vector) $\mathbf{x}=(x_1,x_2,\ldots,x_p)$ 로 주어진다고 하자. 이때 이를 행렬로 묶은 $n\times p$ 행렬 $X_1$과 $1_n\in\mathbb{R^n}$ 에 대해

\[X=(1_n\;\; X_1)\]

의 형태로 Input Matrix 를 정의한다. 또한, 각각의 Input vector에 대응하는 Output 값을 $y_i$들로 표기하고 $n$개의 Output을 묶은 벡터 $Y\in\mathbb{R^n}$ 을 Ouput Vector 라고 정의하자. 여기서 선형회귀란, 다음의 선형 관계식

\[Y=X\beta\]

을 합리적으로 근사할 수 있게 하는 계수(coefficient) 벡터 $\beta = (\beta_0,\beta_1,\ldots,\beta_p)$ 를 찾는 것을 의미한다.

이때 “합리적”임을 판단할 수 있게 하는 가장 기본적인 방법이 최소제곱법이다. 실제 관측값 $y_i$에 대응하는 예측값 $\beta_0+x_1\beta_1+\cdots+x_p\beta_p$의 차이를 오차($\epsilon$)로 정의하는데, 최소제곱법은 이 오차들의 제곱값들의 합을 최소화시키는 계수벡터를 찾는 것이다. 즉,

\[\begin{aligned} \beta &= \mathop{\arg\min}\limits_\beta\sum_{i=1}^n(y_i-\beta_0-\sum_{j=1}^px_{ij}\beta_j)^2\\ &=(Y-X\beta)^\top(Y-X\beta) \end{aligned}\]

여기서 $(Y-X\beta)^\top(Y-X\beta)$ 의 값을 RSS(Residual Sum of Squares) 라고 정의하기도 한다. 이때 행렬미분을 이용하면 최소화 조건을 다음과 같이 얻을 수 있는데,

\[\frac{\partial RSS}{\partial\beta} = -2X^\top(Y-X\beta) = 0 \\ X^\top Y= X^\top X\beta\]

아래 식을 정규방정식^{normal equation}이라 하며 정규방정식의 해

\[\hat{\beta}=(X^\top X)^{-1}X^\top Y\]

를 최소제곱인자라고 한다.

정사영으로서의 최소제곱법

앞에서 구한 최소제곱인자를 이용하여 $Y$를 추정한 벡터를 $\hat{Y}$ 라고 하면,

\[\hat{Y}=X\hat{\beta}=X(X^\top X)^{-1}X^\top Y\]

로 둘 수 있다. 이때 $\hat{Y}$ 는 행렬 $X$ 뒤에 벡터 $\hat{\beta}$ 가 곱해진 꼴이므로, 이는 $X$의 열벡터들의 선형결합이므로, 열공간 $col(X)$ 으로부터 생성되는 원소이다.
또한, 벡터 $Y-\hat{Y}$를 생각하면 이는

\[\begin{aligned} X^\top(Y-\hat{Y}) &= X^\top Y-X^\top X(X^\top X)^{-1}X^\top Y \\ &= 0 \end{aligned}\]

이므로, $X$의 열공간과 직교하는 벡터임을 알 수 있다. 이를 그림으로 표현하면 아래와 같은데,

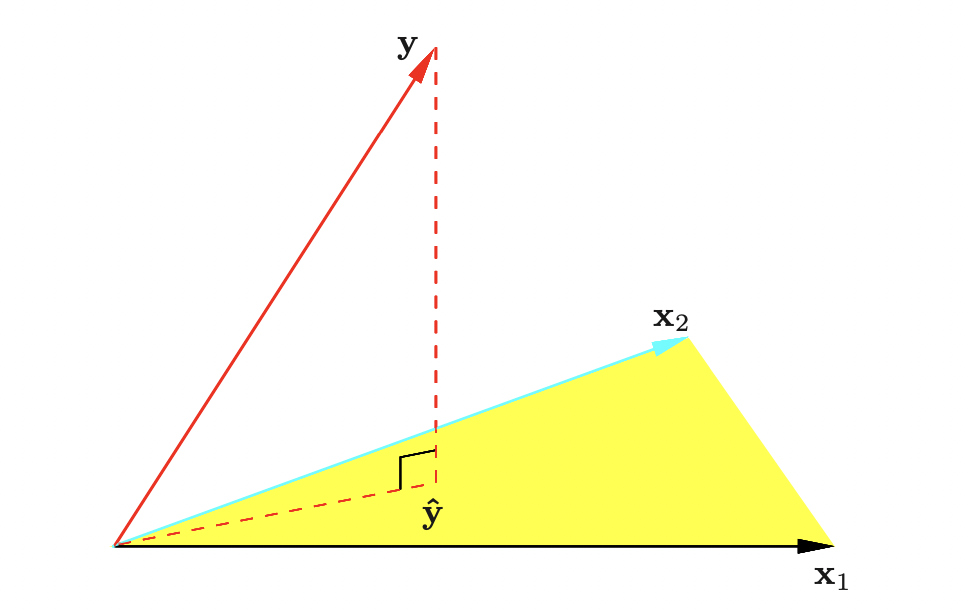
여기서 우리는 예측값 벡터 $\hat{Y}$가 $Y$를 $X$의 열공간으로 정사영시킨것과 같은 것임을 알 수 있다. 또한, 이때 $H=X(X^\top X)^{-1}X^\top$ 을 Hat Matrix 라고 하며 $Y$를 정사영시킨다고도 하여 정사영행렬이라고도 한다.

Shrinkage Regression

앞서 살펴본 최소제곱법은 변수가 많아질 경우 과적합 방지를 위해 변수의 수를 제한해야하는 문제가 발생한다. 그러나 변수의 수(p, 하이퍼파라미터로 생각)를 제한하는 것은 discrete한 과정이고(하이퍼파라미터가 불연속이므로) 변수 제거의 과정에서 분산이 자칫 과도하게 커질 위험이 있다. 또한, 행렬 $X^\top X$ 비정칙(singular)일 경우 역행렬이 존재하지 않는 경우 계산의 어려움 역시 존재한다. 따라서 이러한 문제들을 해결하기 위해 최적화 문제에 규제항을 추가하여 계산하는 방법이 고안되었는데, 대표적으로 Ridge, Lasso 회귀를 살펴보고자 한다.

Ridge Regression

릿지 회귀는 최소제곱법의 최적화 문제에 L2 규제항을 추가하는 것이다. 즉,

\[\Vert\beta\Vert_2^2=\sum_{j=1}^p\beta_j^2\]

을 추가하여 다음과 같은 최적화문제의 해를 회귀게수로 삼는다.

\[\hat{\beta}^{Ridge} = \mathop{\arg\min}\limits_\beta[(Y-X\beta)^\top(Y-X\beta)+\lambda\Vert\beta\Vert_2^2]\]

여기서 $\lambda\geq 0$ Lagrange Multiplier로 사용된 상수이다. 이때 위 최적화 문제를 행렬미분을 이용해 풀면

\[\hat{\beta}^{Ridge}=(X^\top X+\lambda\mathbf{I})^{-1}X^\top Y\]

가 됨을 확인할 수 있고, 이는 비정칙행렬 문제를 해결할 수 있음 역시 알 수 있다.
또한, Singular Value Decomposition(특이값 분해)를 이용해면 $X=UDV^\top$ 으로 표현가능한데, 이때 $V$는 직교행렬이고 $U^\top U=I$가 성립하며 $D$는 고유값들로 이루어진 $p\times p$ 대각행렬이다. 만일 X의 고유값들을 $d_1\geq d_2\geq\cdots\geq d_p\geq 0$ 으로 두면 릿지 회귀의 예측벡터 $\hat{Y}$는 다음과 같이 표현된다.

\[\begin{aligned} \hat{Y}=X\hat{\beta}^{Ridge} &= X(X^\top X+\lambda\mathbf{I})^{-1}X^\top Y\\ &=UD(D^2+\lambda\mathbf{I})^{-1}DU^\top Y\\ &=\sum_{i=1}^p\mathbf{u_i}\frac{d_i^2}{d_i^2+\lambda}\mathbf{u_i^\top}Y \end{aligned}\]

여기서 각 벡터 $\mathbf{u_i}$는 $U$의 열벡터들을 의미한다. 릿지 회귀모형의 설정에서 우리는 $\lambda$ 를 양수로 설정했으므로, 마지막 식의 $d_i^2/(d_i^2+\lambda)$ 는 1보다 작게 된다. 따라서 릿지 회귀에서는 선형회귀와 같이 예측값을 계산하는 과정에서 별도의 수축(shrinkage)이 발생하고, 그 비율은 $d_i^2/(d_i^2+\lambda)$ 에 비례함을 알 수 있다.

Lasso Regression

Lasso 회귀는 L2 규제항을 사용한 릿지회귀와 달리, L1 규제항을 사용하여 다음과 같이 표현된다.

\[\hat{\beta}^{Lasso} = \mathop{\arg\min}\limits_\beta[(Y-X\beta)^\top(Y-X\beta)+\lambda \sum_{j=1}^p\vert \beta_j\vert ]\]

또한, 위 문제는 아래와 동치이다.

\[\hat{\beta}^{Lasso} = \mathop{\arg\min}\limits_\beta(Y-X\beta)^\top(Y-X\beta)\\ \text{subject to } \sum_{j=1}^p\vert \beta_j\vert \leq t\]

그러나 릿지 회귀와 달리 Lasso 문제는 Closed form의 해를 찾을 수 없으므로 다른 알고리즘을 이용해 계산하게 된다. Lasso의 중요한 특징 중 하나로, 제약조건에서의 $t$ 값의 설정에 따라 변수 선택이 이루어진다는 특징이 있다.
최소제곱법을 이용해 얻은 회귀계수들로 $t_o=\sum_j\vert \hat{\beta_j}\vert $ 를 계산했다고 하자. 만일 제약조건의 $t$가 $t_0$보다 크다면, 위 제약은 무효하게 되므로 Lasso 회귀와 최소제곱법이 동일한 결괴를 가짐을 알 수 있다. 반면 반대의 경우, 예컨대 $t=t_0/2$로 주어진다면 최소제곱법 회귀계수들은 50%가량 축소되게 된다. 이때 변수가 선택되 원리는 다음 살펴볼 Least Angle Regression 과정에서 알 수 있다.

Least Angle Regression(LAR)

LAR은 일반적인 회귀분석에서의 전진선택법과 유사하게, 변수들을 하나씩 추가하면서 모형을 생성해나가는 회귀분석 방법이다. LAR의 알고리즘은 다음과 같다.

LAR Algorithm

1. 초기 회귀계수들은 $\mathbf{\beta=0}$ 으로 두고, 잔차벡터를 $\mathbf{r=Y-\bar{Y}}$ 로 둔다 (평균이 0이 되도록).
2. 변수 $\mathbf{x_i}$ 들 중 $\mathbf{r}$ 과의 상관계수가 가장 높은 $\mathbf{x_j}$ 룰 첮는다.
3. $\mathbf{x_j}$ 에 대응하는 $\beta_j$ 의 부호는 2에서의 상관계수의 부호로 설정하고, 크기(절댓값)는 점차 증가시킨다. 이때 다른 변수 $\mathbf{x_k}$ 가 현재 단계의 잔차벡터와 같은 크기의 상관계수를 가지게 될 때 까지만 증가시킨다.
4. $\mathbf{x_j,x_k}$ 만 포함하여 최소제곱인자들을 구하고, 각각의 계수 $\beta_j,\beta_k$를 각 최소제곱인자들의 부호의 방향으로 증가/감소 시킨다. 증가/감소 과정은 다른 변수 $\mathbf{x_l}$ 이 현재 단계의 잔차벡터와 같은 크기의 상관계수를 가지게 될 때 까지 이루어진다.
5. 4번 과정을 계속 반복하여, $\min(n-1,p)$ 단계 이후 종료한다.
6. 이때, 반복 과정에서 0이 되는 회귀계수가 생기면 해당 변수를 제거하고 그 단계의 최소제곱인자의 부호(방향)을 다시 계산한다.

위 알고리즘에서 5단계까지의 알고리즘을 일반적인 LAR이라고 하며, 6단계 조건이 추가된 것을 Lasso Modification 이라고 한다. 신기한(?) 것은 6단계를 추가함으로써 Closed form이 없는 Lasso 회귀문제를 계산할 수 있다는 것이다. 대략적인 이유를 살펴보면 다음과 같다.

LAR vs. Lasso

LAR을 수행하는 알고리즘 중 어떤 단계에서의 Active set(해당 단계에서 유효한 변수 index들의 집합)을 $A$ 라고 하자. LAR 알고리즘에서는 상관계수를 계산해야하는데, 변수들과 잔차가 모두 표준화되어있다고 가정하여, 상관계수와 내적을 동일하게끔 하자(계산의 편의를 위해).
해당 단계에서 (현재) 잔차벡터를 $\mathbf{Y-X\beta}$ 라고 두자. 이때 같은 단계($A$)에 포함된 변수들은 그 단계의 잔차벡터와 동일한 크기의 상관계수를 가지므로 (알고리즘 3,4단계에서 상관계수가 같아질 때 다음 단게로 넘어감을 확인하자), 다음으로 표현할 수 있다.

\[\mathbf{x_j^\top(Y-X\beta)}=\gamma\cdot s_j,\quad \forall j\in A \tag{1}\]

($s_j$는 부호를 나타냄 : $s_j = -1$ or $1$, $\gamma$ 는 공통값임을 의미함)
또한, 해당 단계에 포함되지 않는 다른 변수들의 경우 (현재) 잔차벡터와의 상관계수의 크기가 더 작다. 즉,

\[\vert \mathbf{x_k^\top(Y-X\beta)}\vert \leq\gamma,\quad\forall k\notin A\]

성립한다. 반면, Lasso 최적화 식을 살펴보면

\[R(\beta) = \Vert\mathbf{Y-X\beta}\Vert_2^2+\lambda\Vert\beta\Vert_1\]

을 최적화하는 것이 Lasso 문제인데, 주어진 $\lambda$ 에 대한 Lasso 회귀의 Active set이 $B$로 주어진다고 하자. 이때 $j\in B$에 대해 $\beta_j$로 위 식의 양변을 미분하면 다음 정상성 조건

\[\mathbf{x_j^\top(Y-X\beta)}=\frac{\lambda}{2}\cdot sgn(\beta_j)\quad j\in B \tag{2}\]

을 얻을 수 있다. 이때 식 (1)과 (2)를 비교해보면, Lasso 회귀계수의 부호와 LAR의 상관계수 부호가 동일할 경우 두 식은 동치임을 알 수 있다. 그런데 만일 LAR 알고리즘에서 6번 조건이 없는 경우 특정 회귀계수가 양수에서 음수로 전환되거나 음수에서 양수로 전환되는 문제가 발생한다. 그러나 Lasso 회귀에서는 부호의 전환이 발생하지 않기 때문에, 0에 도달하는 회귀계수를 아예 제거하는 6번 조건을 추가하게 되는 것이다. 즉, 6번 조건의 추가로 인해 Lasso와 LAR이 동치가 된다. 회귀문제에서 변수의 수가 샘플 수보다 훨씬 큰 경우, 위 동치관계를 이용하면 더 속도가 빠른 LAR 알고리즘을 사용하게 된다.

References

• Hastie, T., Tibshirani, R., Friedman, J. H., & Friedman, J. H. (2009). The elements of statistical learning: data mining, inference, and prediction (Vol. 2, pp. 1-758). New York: springer.